线性回归(Linear Regression)
从这篇文章開始。主要介绍机器学习的一些列基本算法,本文介绍线性回归问题,以及利用最小均方和梯度下降解决线性回归问题。
(下面内容是依据斯坦福大学ng教授的机器学习公开课总结的内容)
监督学习:即训练数据中既包括了输入数据又包括了相应于这个是输入数据的正确的输出结果。
回归问题:当给出了输入数据后,预測正确的输出结果。线性回归函数
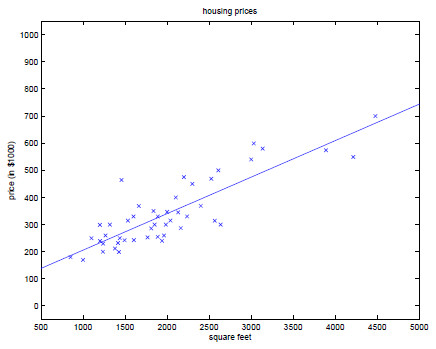
首先考虑一个问题:我们须要预測自己房屋的价格。如今拥有的数据仅仅是几十个房屋样本价格,例如以下图所看到的。如何依据这些房屋的面积以及价格来预測我们自己房屋的价格呢?
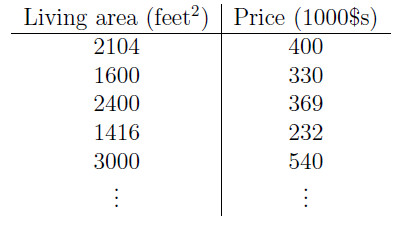 为了更加直观的将已知样本房屋的价格表示出来,我们将上述数据标注在坐标系中。例如以下图:
为了更加直观的将已知样本房屋的价格表示出来,我们将上述数据标注在坐标系中。例如以下图: 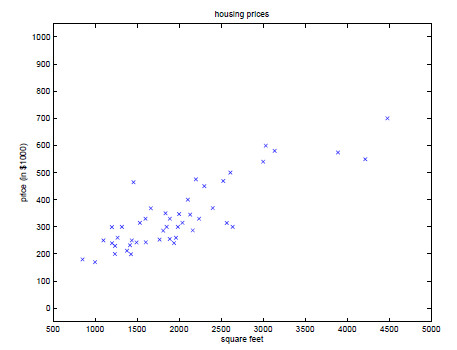 由图我们能够看出,点的分布大致环绕在一条直线周围。因此。我们能够用一个线性函数表示房屋的面积与房屋的价格的相应关系。流程大致例如以下:
由图我们能够看出,点的分布大致环绕在一条直线周围。因此。我们能够用一个线性函数表示房屋的面积与房屋的价格的相应关系。流程大致例如以下: 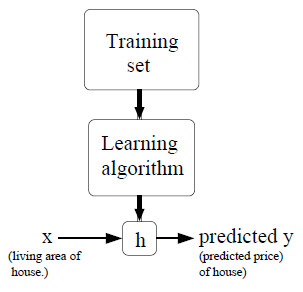 利用训练数据+学习算法得到一个函数h,然后将待预測的房屋面积输入,就可以得到预測的房价。
利用训练数据+学习算法得到一个函数h,然后将待预測的房屋面积输入,就可以得到预測的房价。 首先介绍详细字母代表的含义:
- m:训练数据的总数。
- x:输入值
- y:输出值
- (x,y):训练样本
- (x(i),y(i)):训练样本中的第i对值
为了使得问题更加具有一般性。我们将上面的样例进行扩充成例如以下表格:
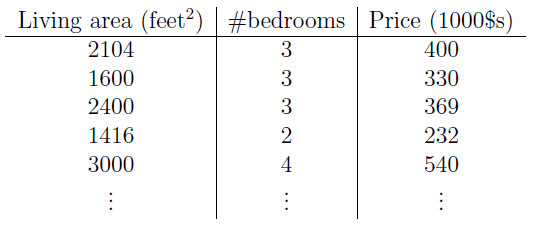
如今我们如果输出值和输入值之间相应的关系为线性函数:
- hθ(x)=θ0+θ1x1+θ2x2
上面的式子为了便于表达,如果x0=1,因此,能够写成:
- hθ(x)=θ0x0+θ1x1+θ2x2=∑ni=0θixi=θTX
如今,当我们有了測试集,如何来预測參数θ?,我们的目的就是使得预測结果尽量接近与真实的结果,因此。在全部的训练集上。我们须要使得该函数的输出结果尽量可能接近真实值,也就是使得差量最小。因此能够表示为例如以下的形式:
- J(θ)=1/2∑mi=0(hθ(x(i))−y(i))2
这个表达形式能够表现出预測值和真实值的平方差量,当中前面的1/2主要是为了后面的求导计算方便。m表示的是全部的训练数据总数量。到这里,我们表示出了误差函数。也就是损失函数。我们的目标是最小化损失函数J(θ),用到的方法是梯度下降法。
梯度下降(gradient descent)
首先我们考虑一个实际的情景,当我们站在山腰的时候。假设我们想最快到达山地,我们首选的方法当然是找坡度最大的地方,即梯度的方向。例如以下图所看到的:
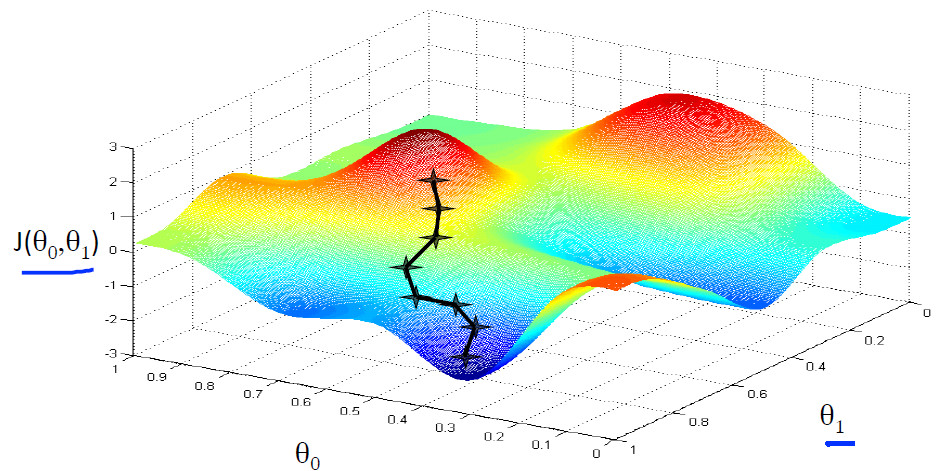 可是,我们会发现一个问题。那就是当我们所处的位置不同的时候,就会走到不同的最低位置,即会出现局部最优。而不是寻找的全局最优值。例如以下图所看到的:
可是,我们会发现一个问题。那就是当我们所处的位置不同的时候,就会走到不同的最低位置,即会出现局部最优。而不是寻找的全局最优值。例如以下图所看到的: 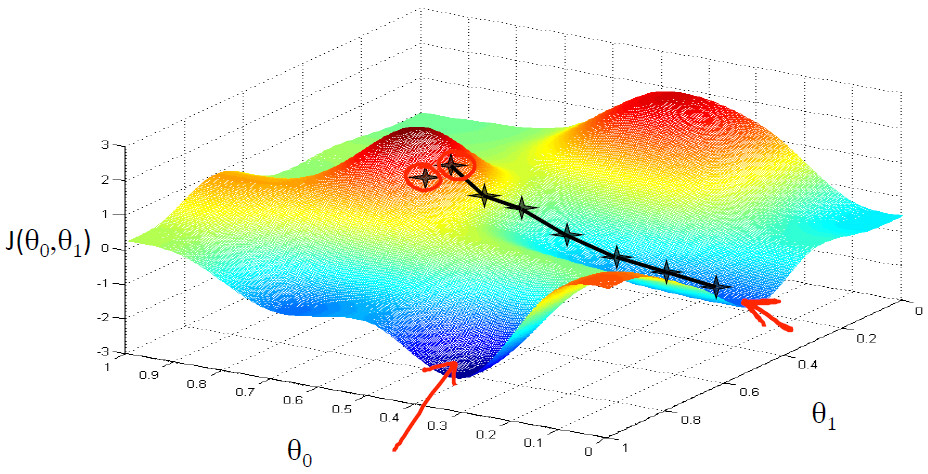 事实上,现实我们遇见的现实问题大多仅仅有一个最小值。因此,不会走入局部最优值。比如本实例图像例如以下所看到的:
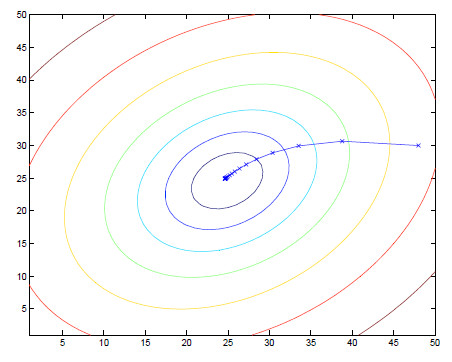
事实上,现实我们遇见的现实问题大多仅仅有一个最小值。因此,不会走入局部最优值。比如本实例图像例如以下所看到的: 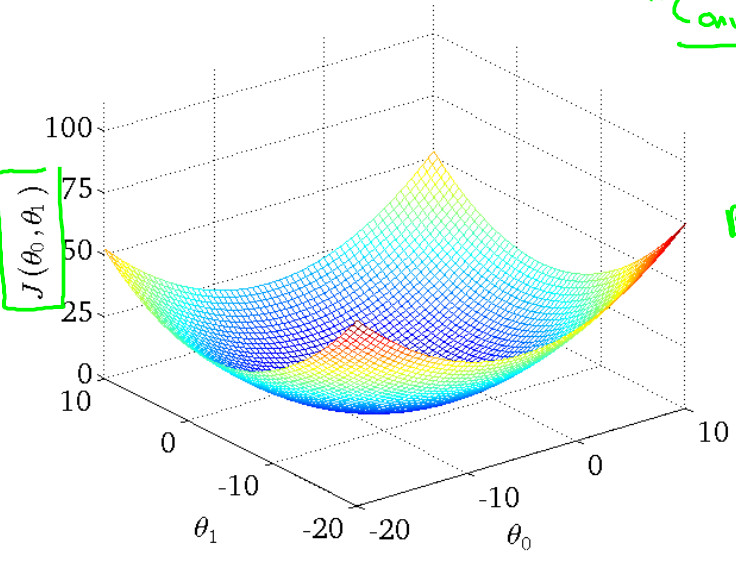 如今。依据上图能够看出我们须要做的就是不断地更新θ(此处的为一个向量。包含θ1和θ2)值,得到到达最小值时候的θ。更新的方法例如以下,即求偏导后沿着偏导数数的方向进行更新。
如今。依据上图能够看出我们须要做的就是不断地更新θ(此处的为一个向量。包含θ1和θ2)值,得到到达最小值时候的θ。更新的方法例如以下,即求偏导后沿着偏导数数的方向进行更新。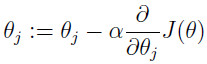 该表达式表示对θi(包含θ1和θ2)更新。当中的α表示更新不发的大小(假设太大可能直接越过了最小值,假设太小,迭代速度太慢。代价太大)。将J带入后计算例如以下:
该表达式表示对θi(包含θ1和θ2)更新。当中的α表示更新不发的大小(假设太大可能直接越过了最小值,假设太小,迭代速度太慢。代价太大)。将J带入后计算例如以下: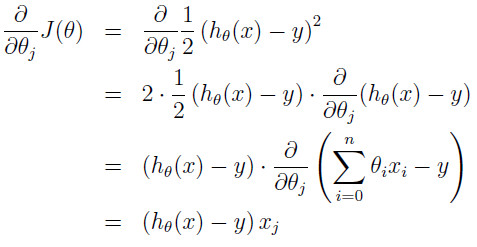 最后结果为:
最后结果为: 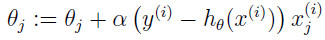 这个规则称为
这个规则称为最小均方(LMS,least mean squares)更新规则 对于以上的式子进行充分直到得到结果就可以。当中反复的形式有两种,一种称作批梯度下降(batch gradient descent)和随机梯度下降(stochastic gradient descent)。 批梯度下降(batch gradient descent)
批梯度下降即每次更新一个參数的一步时候,都须要将全部的数据计算一遍,算法例如以下:
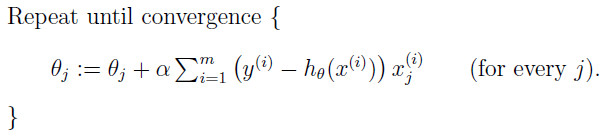 非常明显,这个算法当训练数据集非常大的时候。会导致算法变慢,时间复杂度太大。因此。一般用的比較少。
非常明显,这个算法当训练数据集非常大的时候。会导致算法变慢,时间复杂度太大。因此。一般用的比較少。 随机梯度下降(stochastic gradient descent)
随机梯度下降主要是对以上算法的优化,每一步參数的更新。仅仅看训练数据集中的一个训练数据,算法例如以下:
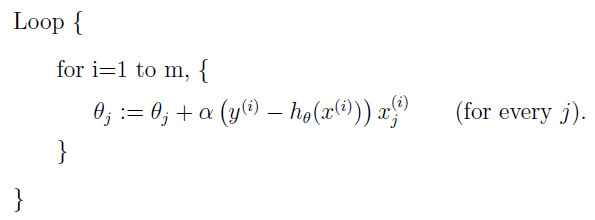
利用以上的算法更新开头提出的问题的解法过程图像和终于结果图像例如以下:
个人博客:http://www.houlaizhexq.com。http://houlaizhexq.github.io/